GSQT – Tiến sĩ Phạm Sĩ Nam, giảng viên Đại học Sài Gòn, thành viên Ban soạn thảo chương trình Giáo dục phổ thông mới môn Toán, đã đề xuất dạy xác suất từ lớp 2 tại hội thảo xu hướng giáo dục trên thế giới và Việt Nam vừa qua.

Trước những phản hồi gần đây liên quan đến vấn đề này, ông Nam dành thời gian chia sẻ sâu hơn: “Xác suất, thống kê là cái đi vào đời sống nhiều nhất. Nhiều người cho rằng đây là những nội dung khó, trừu tượng vì chương trình hiện hành xác suất chỉ được dạy vào năm lớp 11, còn thống kê cũng được học rãi rác từ tiểu học, lớp 7, lớp 10.”

“Với chương trình mới, dạy xác suất từ lớp 2 không có nghĩa là lôi chương trình từ lớp 11 để dạy cho lớp 2 mà đó là tên của mạch kiến thức. Có những kiến thức đòi hỏi một tiến trình dạy cũng như có quá trình để học sinh trải nghiệm”.

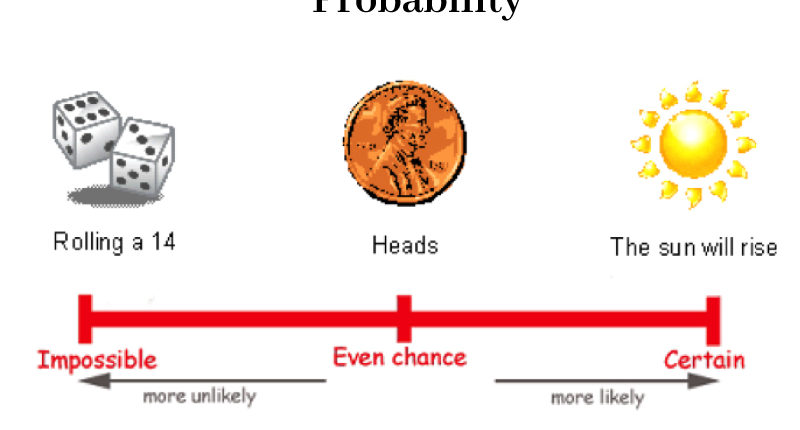
Dạy xác suất từ lớp 2 thì học những khái niệm cơ bản của xác suất như “chắc chắn” hay “không chắc chắn”. Ví dụ, trời đang mưa khi ra ngoài trời thì chắn chắn bị ướt hay 100% bị ướt. Xác suất chỉ trả lời những câu hỏi đó chứ không phải là những bài tính toán to tác như lớp 11. Đồng thời, không chỉ học ở lớp 2, mà lớp 3, 4 và các bậc học cao hơn cũng phải có tính liên tục, không làm đứt mạch mà học sinh lĩnh hội.

Cũng theo ông Nam, chương trình hiện hành theo quan điểm tiếp cận nội dung nhằm trả lời câu hỏi muốn học sinh biết gì và chúng ta quan điểm những em nào tiếp thu nhiều đơn vị kiến thức là giỏi, do đó dẫn đến tình trạng bất cập khi có những em toàn điểm 10 môn Vật lý nhưng không biết mắc một bảng điện, hay Toán đầy mình nhưng đưa ra một bản đồ hoặc hình ảnh bảo ước lượng diện tích vùng đó bao nhiêu thì các em không tính được.

Tiến sĩ Nam khẳng định chương trình mới sẽ gắn toán học với cuộc sống. Ông dẫn chứng bằng cách đặt ra câu hỏi từ thực tế rằng tại sao vỏ lon bia có dạng hình trụ mà không dùng hình cầu và vì sao Grab lấn át taxi truyền thống, sau đó khẳng định kiến thức Toán học có thể lý giải.